Tanmay Rajpurohit
Education
-
Ph.D. 2018
Ph.D. in Aerospace Engineering
Georgia Inst. of Technology, Atlanta
-
M.S. 2018
Masters of Science in Computer Science
Georgia Inst. of Technology, Atlanta
-
M.S. 2016
Masters of Science in Mathematics
Georgia Inst. of Technology, Atlanta
Action cannot destroy ignorance, for it is not in conflict with or opposed to ignorance. Knowledge does verily destroy ignorance as light destroys deep darkness.
Research
Research Summary
Stochastic dissipativity : Many physical and engineering systems are open systems, that is, the system behavior is described by an evolution law that involves the system state and the system input with, possibly, an output equation wherein past trajectories together with the knowledge of any inputs define future trajectories (uniquely or nonuniquely) and the system output depends on the instantaneous (present) values of the system state. Dissipativity theory is a system-theoretic concept that provides a powerful framework for the analysis and control design of open dynamical systems based on generalized system energy considerations. In particular, dissipativity theory exploits the notion that numerous physical dynamical systems have certain input-output and state properties related to conservation, dissipation, and transport of mass and energy. In light of the fact that energy notions involving conservation, dissipation, and transport also arise naturally for dissipative diffusion processes, it seems natural that dissipativity theory can play a key role in the analysis and control design of stochastic dynamical systems. In addition, robust stability for stochastic dynamical systems with stochastic uncertainty can be analyzed by viewing the uncertain stochastic dynamical system as an interconnection of stochastic dissipative dynamical subsystems. Alternatively, stochastic dissipativity theory can be used to design feedback controllers that add dissipation and guarantee stability robustness in probability allowing stochastic stabilization to be understood in physical terms.
As part of this research we extended classical dissipativity theory to stochastic dissipativity for nonlinear stochastic dynamical systems to address the design of feedbackcontrollers that add dissipation and guarantee stability robustness in probability allowing stochastic stabilization to be understood in physical terms. In addition, we used stochastic dissipativity to quantify stochastic robustness as well as address risk-sensitive disturbance rejection, stability in probability of feedback interconnections, and optimality with averaged performance measures for stochastic dynamical systems. In future research, the plan is to develop connections between stochastic dissipativity and stochastic optimal control to address robust stability and robust stabilization problems involving both stochastic and deterministic uncertainty as well as both averaged and worst-case performance criteria.
Nonlinear-nonquadratic stochastic optimal control:Under certain conditions nonlinear controllers offer significant advantages over linear controllers. This has motivated us to develop a unified framework to address the problem of optimal nonlinear analysis and feedback control for nonlinear stochastic dynamical systems, wherein we considered a feedback stochastic optimal control problem over an infinite horizon involving nonlinear-nonquadratic performance functionals. The performance functionals can be evaluated in closed-form as long as the nonlinear-nonquadratic cost functional considered is related in a specific way to an underlying Lyapunov function that guarantees asymptotic stability in probability of the nonlinear closed-loop system. This Lyapunov function is shown to be the solution of the steady-state stochastic Hamilton-Jacobi-Bellman equation. These results were then used to provide extensions of the nonlinear feedback controllers obtained in the literature that minimize general polynomial and multilinear performance criteria. To show the efficacy of the framework, the results were applied to a pitch axis longitudinal dynamics model of an F-16 Fighter aircraft system with stochastic disturbances.
Stochastic finite-time and partial-state stabilization: The problem of finite-time optimal control has received very little attention in the literature. When the performance functional involves subquadratic terms, the cost criterion pays close attention to the behavior of the state near the origin. My interest in subquadratic cost criteria stems from the fact that optimal controllers for such criteria are sublinear, and thus, exhibit finite settling time behavior. This phenomenon was studied in my dissertation as well as and applied to a spacecraft control problem with one axis of symmetry and with solar pressure captured as a stochastic disturbance.
Our stochastic finite-time stabilization results yield finite interval controllers even though the original cost criterion was defined on the infinite horizon. Hence, one advantage of this approach for certain applications is to obtain finite-interval controllers without the computational complexities of two-point boundary value problems. It is also important to note that if the order of the subquadratic state terms appearing in the cost functional is sufficiently small, then the controllers actually optimize a minimum-time cost criterion. Currently, such results are only obtainable using the maximum principle, which generally does not yield feedback controllers.
Another important extension is the consideration of optimal partial-state stabilization and partial finite-time stabilization, that is, closed-loop stability with respect to part of the closed-loop systems state, which arises in many engineering applications. Specifically, in spacecraft stabilization via gimballed gyroscopes asymptotic stability of an equilibrium position of the spacecraft is sought while requiring Lyapunov stability of the axis of the gyroscope relative to the spacecraft. Alternatively, in the control of rotating machinery with mass imbalance, spin stabilization about a nonprincipal axis of inertia requires motion stabilization with respect to a subspace instead of the origin. The most common application where partial stabilization is necessary is adaptive control, wherein asymptotic stabilization of the closed-loop plant states is guaranteed without necessarily achieving parameter error convergence. As part of our work on stochastic stabilization, we have developed a unified framework to address the problem of optimal nonlinear feedback control for partial stability and partial-state stabilization of stochastic dynamical systems.
Adaptive control with low-frequency learning and fast adaptation: While adaptive control has been used in numerous applications to achieve system performance without excessive reliance on system models, the necessity of high-gain learning rates for achieving fast adaptation can be a serious limitation of adaptive controllers. Specifically, in safety-critical systems involving large system uncertainties and abrupt changes in system dynamics, fast adaptation is required to achieve stringent tracking performance specifications. However, fast adaptation using high-gain learning rates can cause high frequency oscillations in the control response resulting in system instability. To address the problem of achieving fast adaptation using high-gain learning rates for systems with partial state information, we developed an output feedback adaptive control framework for continuous-time, minimum phase multivariable dynamical systems for output stabilization and command following. The approach is based on a nonminimal state-space realization that generates an expanded set of states using the filtered inputs and filtered outputs (along with their derivatives) of the original system, and requires knowledge of only the open-loop system’s relative degree and a bound on the system’s order.
This control architecture was applied to a roll autopilot controller of a guided missile and the longitudinal dynamics of a Boeing 747 airplane. In addition, the adaptive control architecture was applied to the stabilization of a flexible spacecraft. Specifically, we show that a standard adaptive architecture cannot simultaneously achieve a fast convergence rate and obtain a smooth system response. Large adaptive gains lead to a highly oscillatory system response, large control inputs, and unrealistic control input rates. On the other hand, small adaptive gains result in slow convergence rates. However, when our adaptive control architecture is used the system is able to achieve a fast convergence rate and obtain a smooth system response, simultaneously. In addition, the maximum control input and control input rate are decreased and the flexible dynamics of the system were less excited.
Stochastic differential games: Differential games have been studied in various contexts including risk-sensitive control, mathematical finance, and communication networks as well as network resource allocation. The pioneering work on the subject involved a deterministic two-player differential game problem whose solution is characterized by the Hamilton-Jacobi-Isaacs equation. In ongoing research, we have developed a framework that focuses on the role of the Lyapunov function guaranteeing stochastic stability of the differential game and its connection to the steady-state solution of the stochastic Hamilton-Jacobi-Isaacs equation characterizing the optimal nonlinear feedback controller and stopper policies. In order to avoid the complexity in solving the stochastic steady-state, Hamilton-Jacobi-Isaacs equation my framework does not attempt to minimize/maximize a given cost functional, but rather, parameterizes a family of stochastically stabilizing controller and stopper policies that minimizes/maximizes a derived cost functional that provides the flexibility in specifying the control and stopper.
Thermodynamics, control, and large-scale, multi-agent systems: My current research has concentrated on coordinated control of large-scale \textit{stochastic} multi-agent networked systems. In many applications involving multiagent systems, a group of agents are required to agree on certain quantities of interest. In such applications, it is important to develop information consensus protocols for a network of dynamic agents. As part of this ongoing research effort, I am addressing semistable (i.e, Lyapunov stable plus convergent) consensus problems for nonlinear stochastic network systems with switching communication topologies and communication dropouts. In particular, I am developing a thermodynamic-based stochastic control framework in order to consider random communication disturbances between agents in the network, wherein the evolution of each link of the random network follows a Markov process. This will necessitate the development of almost sure consensus of multiagent systems with nonlinear stochastic dynamics under distributed nonlinear consensus protocols. Furthermore, I will relate almost sure consensus of multiple agents over random networks to the semistability notion of the nonlinear stochastic systems. Specifically, using my recent results on stochastic semistability for nonlinear stochastic systems with a continuum of equilibria, I will develop consensus control protocols for multiagent systems in the face of probabilistic variations in the interconnections between agents.
System thermodynamics: As part of my long-term research endeavor I plan to concentrate on the amalgamation of thermodynamics, statistical physics, information theory, and control. Professor Haddad and I have been working on unified framework of system thermodynamics. Specifically, building on the results of Professor Haddad’s 2005 monograph, we are working on a system-theoretic foundation for thermodynamics by combining the two universalisms of thermodynamics and dynamical systems theory under a single umbrella so as to harmonize it with classical mechanics. In particular, we are developing a novel formulation of thermodynamics that can be viewed as a moderate-sized system theory as compared to statistical thermodynamics. This middle-ground theory involves deterministic and stochastic large-scale dynamical system models as well as infinite-dimensional models that bridge the gap between classical and statistical thermodynamics and includes topics on finite-time thermodynamics, critical phase transitions, fluctuation theorems, chemical thermodynamics, and relativistic effects.
Interests
- Nonlinear Analysis and Control
- Stochastic Calculus
- Adaptive Control
- Mathematical Finance
- System Thermodynamics
- Stochatic Differential Games
- Machine Learning
- Robotics
- Biga Data Analytics
- Distributed Network Control
- Information Theory
Research Collaborators
Adviser: Dr. W. M. Haddad
Dr. Haddad has made numerous contributions to the development of nonlinear control theory and its application to aerospace, electrical, and biomedical engineering. His transdisciplinary research in systems and control is documented in over 600 archival journal and conference publications, and 7 books in the areas of science, mathematics, medicine, and engineering.
Dr. Haddad is an NSF Presidential Faculty Fellow; a member of the Academy of Nonlinear Sciences; an IEEE Fellow; and the recipient of the 2014 AIAA Pendray Aerospace Literature Award. His research is on nonlinear robust and adaptive control, nonlinear systems, large-scale systems, hierarchical control, hybrid systems, stochastic systems, thermodynamics, network systems, systems biology, and mathematical neuroscience.
Publications
Filter by type:
A Dynamical Systems Theory of Thermodynamics: Deterministic and Stochastic Perspectives
Dissipativity Theory for Nonnegative and Compartmental Dynamical Systems with Time Delay
Abstract
Nonnegative and compartmental dynamical system models are derived from mass and energy balance considerations that involve dynamic states whose values are nonnegative. These models are widespread in engineering and life sciences and typically involve the exchange of nonnegative quantities between subsystems or compartments wherein each compartment is assumed to be kinetically homogeneous. However, in many engineering and life science systems, transfers between compartments are not instantaneous and realistic models for capturing the dynamics of such systems should account for material in transit between compartments. Including some information of past system states in the system model leads to infinite-dimensional delay nonnegative dynamical systems. In this paper we develop new notions of dissipativity theory for nonnegative dynamical systems with time delay using linear storage functionals with linear supply rates. These results are then used to develop general stability criteria for feedback interconnections of nonnegative dynamical systems with time delay.
Output Feedback Adaptive Control with Low-Frequency Learning and Fast Adaptation
Abstract
In safety-critical systems involving large system uncertainties and abrupt changes in system dynamics, fast adaptation is required to achieve stringent tracking performance specifications. However, fast adaptation using high-gain learning rates can cause high frequency oscillations in the control response resulting in system instability. This paper develops an output feedback adaptive control framework for continuous-time, minimum phase multivariable dynamical systems for output stabilization and command following to address the problem of achieving fast adaptation using high-gain learning rates for systems with partial state information. The proposed framework uses a controller architecture involving a modification term in the update law that filters out the high-frequency content in the control response while preserving uniform boundedness of the system error dynamics. The approach is based on a nonminimal state-space realization that generates an expanded set of states using the filtered inputs and filtered outputs, as well as their derivatives, of the original system, and requires knowledge of only the open-loop system’s relative degree and a bound on the system’s order.
Dissipativity Theory for Nonlinear Stochastic Dynamical Systems: Input-Output and State Properties, and Stability of Feedback Interconnections
Abstract
In this paper, we develop stochastic dissipativity theory for nonlinear dynamical systems using basic input-output and state properties. Specifically, a stochastic version of dissipativity using both an input-output as well as a state dissipation inequality in expectation for controlled Markov diffusion processes is presented. The results are then used to derive extended Kalman–Yakubovich–Popov conditions for characterizing necessary and sufficient conditions for stochastic dissipativity of stochastic dynamical systems using two-times continuously differentiable storage functions. In addition, feedback interconnection stability in probability results for stochastic dynamical systems are developed thereby providing a generalization of the small gain and positivity theorems to stochastic systems.
Lyapunov and Converse Lyapunov Theorems for Stochastic Semistability
Abstract
This paper develops Lyapunov and converse Lyapunov theorems for stochastic semistable nonlinear dynamical systems. Semistability is the property whereby the solutions of a stochastic dynamical system almost surely converge to (not necessarily isolated) Lyapunov stable in probability equilibrium points determined by the system initial conditions. Specifically, we provide necessary and sufficient Lyapunov conditions for stochastic semistability and show that stochastic semistability implies the existence of a continuous Lyapunov function whose infinitesimal generator decreases along the dynamical system trajectories and is such that the Lyapunov function satisfies inequalities involving the average distance to the set of equilibria.
Nonlinear-Nonquadratic Optimal and Inverse Optimal Control for Stochastic Dynamical Systems
Abstract
In this paper, we develop a unified framework to address the problem of optimal nonlinear analysis and feedback control for nonlinear stochastic dynamical systems. Specifically, we provide a simplified and tutorial framework for stochastic optimal control and focus on connections between stochastic Lyapunov theory and stochastic Hamilton-Jacobi-Bellman theory. In particular, we show that asymptotic stability in probability of the closed-loop nonlinear system is guaranteed by means of a Lyapunov function which can clearly be seen to be the solution to the steady-state form of the stochastic Hamilton-Jacobi-Bellman equation, and hence, guaranteeing both stochastic stability and optimality. In addition, we develop optimal feedback controllers for affine nonlinear systems using an inverse optimality framework tailored to the stochastic stabilization problem. These results are then used to provide extensions of the nonlinear feedback controllers obtained in the literature that minimize general polynomial and multilinear performance criteria.
Partial-State Stabilization and Optimal Feedback Control for Stochastic Systems
Abstract
In this paper, we develop a unified framework to address the problem of optimal nonlinear analysis and feedback control for partial stability and partial-state stabilization of stochastic dynamical systems. Partial asymptotic stability in probability of the closed-loop nonlinear system is guaranteed by means of a Lyapunov function that is positive definite and decrescent with respect to part of the system state which can clearly be seen to be the solution to the steady-state form of the stochastic Hamilton-Jacobi-Bellman equation, and hence, guaranteeing both partial stability in probability and optimality. The overall framework provides the foundation for extending optimal linear-quadratic stochastic controller synthesis to nonlinear-nonquadratic optimal partial-state stochastic stabilization. Connections to optimal linear and nonlinear regulation for linear and nonlinear time-varying stochastic systems with quadratic and nonlinear-nonquadratic cost functionals are also provided. Finally, we also develop optimal feedback controllers for affine stochastic nonlinear systems using an inverse optimality framework tailored to the partial-state stochastic stabilization problem and use this result to address polynomial and multilinear forms in the performance criterion.
Stochastic Finite-Time Partial Stability, Partial-State Stabilization, and Finite-Time Optimal Feedback Control
Abstract
In many practical applications, stability with respect to part of the system's states is often necessary with finite-time convergence to the equilibrium state of interest. Finite-time partial stability involves dynamical systems whose part of the trajectory converges to an equilibrium state in finite time. In this paper, we address finite-time partial stability in probability and uniform finite-time partial stability in probability for nonlinear stochastic dynamical systems. Specifically, we provide Lyapunov conditions involving a Lyapunov function that is positive definite and decrescent with respect to part of the system state, and satisfies a differential inequality involving fractional powers for guaranteeing finite-time partial stability in probability. In addition, we show that finite-time partial stability in probability leads to uniqueness of solutions in forward time and we establish necessary and sufficient conditions for almost sure continuity of the settling-time operator of the nonlinear stochastic dynamical system. Next, we develop a unified framework to address the problem of optimal nonlinear analysis and feedback control design for finite-time partial stochastic stability and finite-time, partial-state stochastic stabilization. Finite-time partial stability in probability of the closed-loop nonlinear system is guaranteed by means of a Lyapunov function that is positive definite and decrescent with respect to part of the system state and can clearly be seen to be the solution to the steady-state form of the stochastic Hamilton-Jacobi-Bellman equation guaranteeing both finite-time, partial-state stability and optimality. The overall framework provides the foundation for extending stochastic optimal linear-quadratic controller synthesis to nonlinear-nonquadratic optimal finite-time, partial-state stochastic stabilization. In addition, we specialize our results to address the problem of optimal finite-time control for nonlinear time-varying stochastic systems. Finally, we develop optimal feedback controllers for affine nonlinear stochastic systems using an inverse optimality framework tailored to the finite-time, partial-state stochastic stabilization problem and use this result to address finite-time, partial-state stabilizing stochastic controllers that minimize a derived performance criterion.
Dissipativity Theory for Nonnegative and Compartmental Dynamical Systems with Time Delay
Abstract
Nonlinear-Nonquadratic Optimal and Inverse Optimal Control for Stochastic Dynamical Systems
Abstract
Partial-State Stabilization and Optimal Feedback Control for Stochastic Systems
Abstract
Dissipativity Theory for Nonlinear Stochastic Dynamical Systems: Input-Output and State Properties, and Stability of Feedback Interconnections
Abstract
Stochastic Finite-Time Partial Stability
Abstract
Projects
-
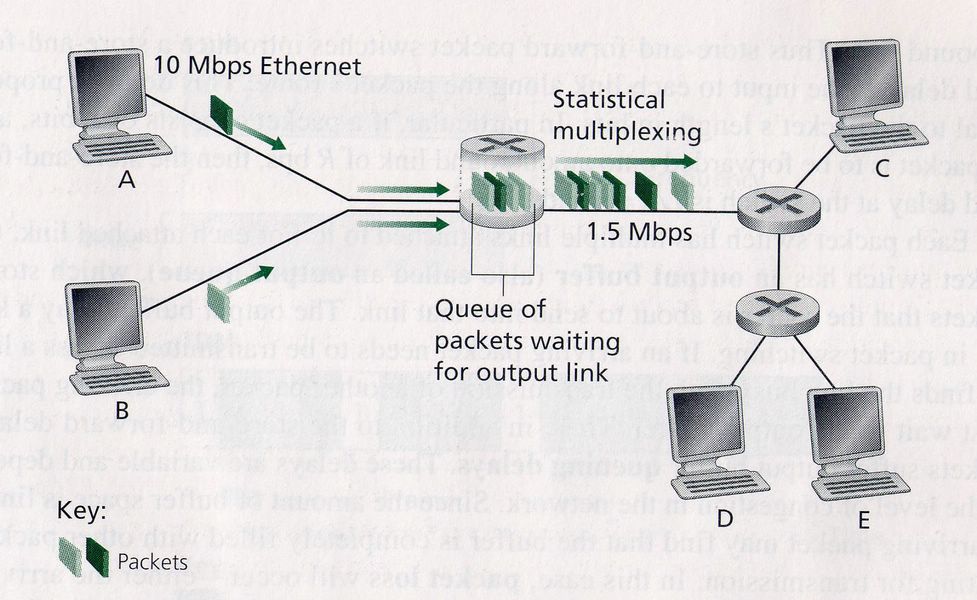
Problem Description: The goal of the project is to address and analyze the following questions
- For a given parameter inputs router throughput and buffer size compare the network efficiency of various Active Queue Management Algorithms (Random Early Detection, Blue and Stochastic Fair Blue, Advanced Random Early Detection etc.) as against the classical FIFO with tail drop through Discrete Event Simulation by analyzing the primary metrics of interest (latency, average buffer occupancy, average packet drop/ retransmission) that eventually preventing TCP congestion collapse.
- Design and implement the same simulation in parallel simulations scheme using deadlock detection and avoidance using Chandy-Misra-Brayant algorithm.
System Under Investigation was computer network, static topology communicating with each other through packet switching mechanism. The SUI was simplified for the simulation purpose to 3 routers (Nodes), 8 Computers, 20,000 packets for some source and destination generated randomly, maximum queue length assumed for each buffer: 10 (i.e. max of 10 packets), throughput rate of the routers is unchanged for the entire simulation, data packets generated from each computer from i.i.d process, and probability of dropping is varied and analysis is performed.
Simulation Architecture was designed for Event Based Simulation with Data packets as Consumer Entity, the nodes of the network i.e. Routers, Gateways, Switches etc. as Resource Entity, and Queue at each node as Queue Entity. Traveling across the network by each consumer entity obeying the first hop routing algorithm at each node are modeled as Activities.
Results and Conclusion
- Event Based Simulations performed for analyzing various metrics of interest
- FIFO & RED is not feasible for Low-Rate-Denial-of-Service-Attacks
- RRED provides and adaptive framework to actively optimize according to service attacks
- Average Queue Length is higher in RRED than RED
- Packages Served is maximum in RRED. RED has initially worst performance
-

Problem Description: Goal of the project is to estimate the improvement on traffic efficiency, by reduction in average travel time, due to synchronization of successive signal, through discrete-event-simulation (DES).
System Under Investigation was segment of Peachtree St between 10th St. and 14th St. comprising of 3 signals, at every signal there is traffic on both direction, i.e. East-West and North-South, the signal timing Red-Green-Yellow is fixed apriori, and also assumed ‘spill over’ effect.
Simulation Architecture was designed for Event Based Simulation with Vehicles as Consumer Entity, Signals, Road (may drop this if `spill over' effect is not simulated) as Resource Entity, and Queue at each signal as Queue Entity. Traveling usage of segment of Peachtree St by each consumer entity obeying the signal constraints are modeled as Activities.
Results and Conclusion
- The average travel time has been significantly reduced while using the signal synchronized scheme
- With little but more effort optimized value for the signal cycle time and the synchronization offset value can further improve the traffic efficiency.
- Confidence Interval has been significantly improved in the signal synchronized scheme. Thereby the synchronization provides better and accurate estimation of average travel time
-

Summary: Every year, thoudands of international students go though arduous task of collecting information of prospective colleges in the US. The availability of information has only made task more complex. This is followed by stressful and expensive application process, which may or may not result in acceptance. Students post their academic background and responses from Universities in online forums. We leveraged that information to create a tool for international students that helps them make better college choices.
The Data: There are three sources of data: first, the online forum data which includes the results of an application to a university program along with the applicant's GRE score, TOEFL score, GPA, undergraduate university ranking and other factors. This data was scrapped, translated, cleaned and normalized. The second source is the US Department of Education's College Scorecard which provides detailed information of all US colleges. The third source is from the QS Intelligence Unit, which provides university ranking. This information about the colleges was appended to them.
How it Works: Users can interact with the tool through a wen page interface. First, the user is asked to enter their background and interests. Second, the chances of acceptance by Universities is evaluated by training a classifier on forum data and classifying the user input for all colleges. Thrid, this probability of acceptance, along with each University's internal attributes, provides a suitability score for every University. Finally, the top matches are preseted to the user.
Challenges: Chance of admission is a prime factor in a students choice of which University to apply to and important measurable factors determining the chance of admission are the GPA of a student as well as GRE scores, or so we thought. Looking at the admission rate to a Masters program at Duke University (a University with a particularly balanced accept/reject rate in our data set), we are hard pressed to spot a pattern. Part of the reason for this is that GPA scores are reported in different format that works well. And in fact, employing Support Vector Machine with RBF kernel reveals nothing more that a slight increase of admission rate around a GPA reported as 4 and GPAs reported as 10, yeilding an accuracy of 58% reported by the cross-validation used to find the SVM-hyperparameters and an accuracy of 54% on the validation set, barely a perceivable increase over using the prior probability of acceptance of 51%. The remaining features include University ranks and the TOEFL scores.
-

Summary: In this project, we implement the Jacobi iterative method of solving linear system for both dense and sparse matrices. The CSR data structure is used to store sparse matrix. Impact of sparsity is analyzed through comparative analysis between and dense and sparse matrix based on time and space complexity. The convergence criterion for all the iterative algorithms in this paper is tolerance band of 10-10.
Results and Conclusion:
- The space requirement for LU is invariant under varying matrix density as the entire matrix is stored. Sparse Jacobi, on the other hand, uses the CSR storage format which gives significant space savings for sparse atrices. This space complexity, increases linearly with increasing matrix density. However, note that the memory usage becomes prohibitively more expensive than the LU method for densities higher than 0.5. Thus, sparse Jacobi is preferred over LU for densities lesser than 0.5 and LU is preferred subsequently with respect to memory storage.
- As the density increases, the computational complexity remains almost constant for LU and Jacobi. However, for sparse Jacobi, the computational complexitys dependence on density is clearly manifested with the time required increasing with increasing density. The reason for the observed trends in the above graph can be explained by considering the algorithmic complexity. While LU decomposition takes O(n3) flops, the flops required by the Jacobi method is O(n2) per iteration. Further, the flops required by the sparse Jacobi method are O(nnz) per iteration with nnz being the number of non-zero elements. Thus, the required time is lowest for sparse Jacobi and highest for LU decomposition for the case study involving n = 1000.
- The algorithmic complexity is O(nnz) per iteration for sparse Jacobi which means that the computational complexity can be prohibitively high for cases requiring a large number of iterations to converge to the solution.
-

Summary: Implemented the Delaunay triangulation algorithm for grid generation with high efficiency in C, to serve as a library for CFD projects, using MPI protocol to run on PARAM-10000 super computer. Also implemented the post processing graphical visualization in C++ using openGL. Explored the possibility of improving further efficacy by extending the implementation in Java though multi-threading.
-

-

-

Gallery
Contact & Meet Me
- lab: 404-894 3474
- tanmay.rajpurohit@gatech.edu
- tanmay.rajpurohit@gmail.com
- trp7ua
- @tanmayRPurohit
- us.linkedin.com/in/tanmay-rajpurohit









